Compositional
Multi-objective parameter tuning
What is parameter tuning?
\bar{v} \in V
.. is the problem of choosing a set of optimal hyperparameters
f = (f_1, f_2,...,f_m)
\bar{v} = (p_1, p_2,...,p_n)
(\bar{v} )
should be minimized
f_i

- Grid search
- Random search
- Bayesian optimization
- Evolutionary optimization

f = (f_1, f_2)
\bar{v} = (p_1, p_2)
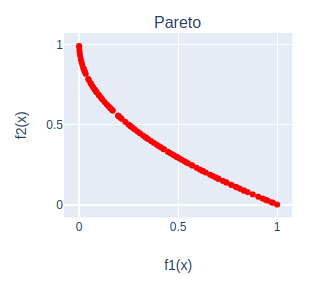
Multi-obj algorithm (NSGA-II)

f = (f_1, f_2)
\bar{v} = (p_1, p_2)
Multi-obj algorithm (NSGA-II)
x400 samples
What the difference?
| Basic | Compositional |
|---|---|
| costly | cheap target function |
| static | adaptive |
| state-of-the-art solution | near-optimal solution |


Classical single
optimization
Multi-/Many-obj
optimization
Compositional
Multi-objective


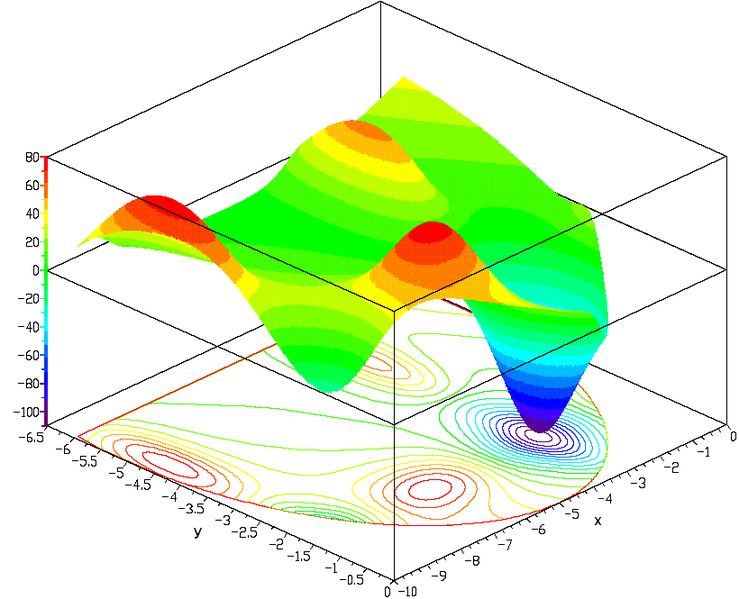



Obj-1
Obj-2
Samples
NSGA-II






Obj-1
Obj-2
Samples
NSGA-II
Decision tree
- Coarse-grained and for use in batch computations.
- Defines inputs and outputs, optionally typed within the inner type system.
- Embeddable in a dependency graph that is constructed by connecting inputs and outputs
- Defines self-describing, strongly-typed configuration.
- Designed for testability and reuse.

The core abstraction is the Solid:
Multi-obj optimization
Good, Fast, Cheap: Pick any two (you can't have all three)
f = (f_1, f_2,...,f_m)
should be minimized
f_i
∀ {i} \in \{ 1,2, .., m\}
- Weighted-sum
- Evolutionary algorithm
\tilde{f} = \textstyle\sum_{i=1}^nw_i*f_i
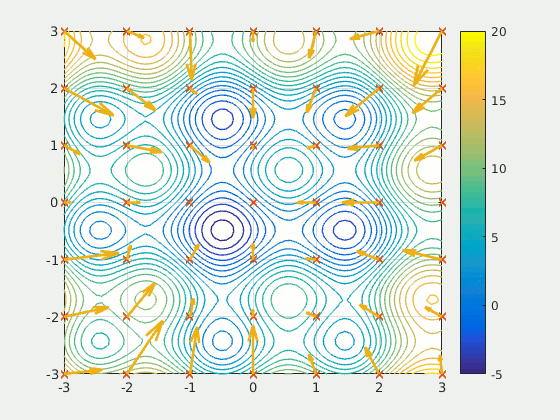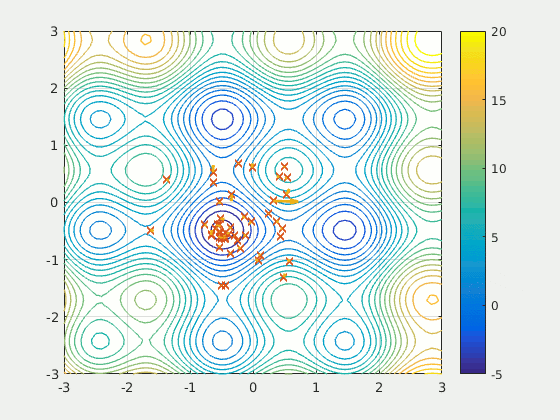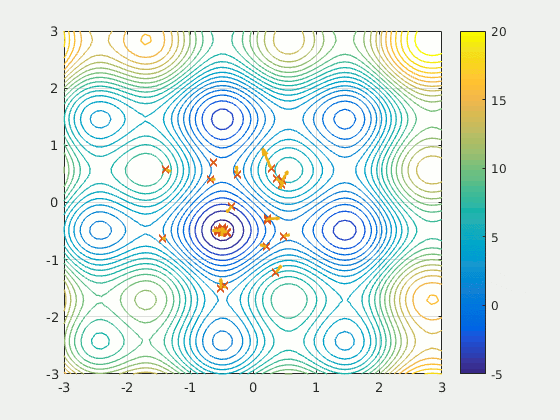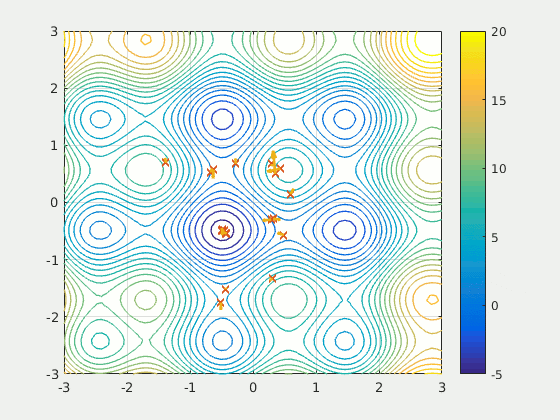
#TODO
- Component class & composition
- Algorithms
- Bayesian optimization
- Polynomial regression
- Reinforcement learning
- Linear regression
- Evolutionary algorithm
class Model(ABC):
@abstractmethod
def build_model(self): pass
@abstractmethod
def validate_model(self): pass
@abstractmethod
def predict_next_configurations(self, amount):
# TODO: Make it `template method` or 'strategy'.
return Configuration
@abstractmethod
def update_data(self, configurations: List[Configuration]):
return self#TODO: Evaluation
- Synthetic problem
- The CEC 2009 problems: Competition
- Zitzler–Deb–Thiele's
- Real-world problem
- Sweet-spots
- Physical simulation
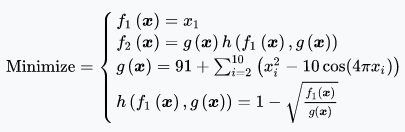
ZDT-4
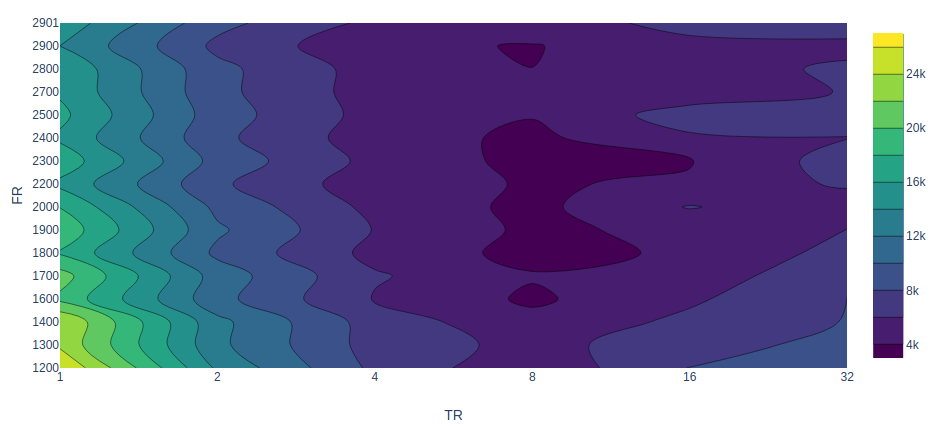
Energy consumption: nanozip